My previous post presumed some understanding not just of the Black-Scholes formula, but also of its derivation; in particular, of the hedging argument whereby the drift in the underlying asset can be ignored. My likely readers at this blog probably do understand this, but some other commentators may not. How to explain? Here, with some trepidation, is an attempt at analogy (I say “with some trepidation” because no analogies are perfect, and this one works best for recreational sailors).
Suppose you are sailing your boat at sea on a misty day. The mist briefly clears and in the distance you glimpse your friends, who are drift fishing on their boat. You quickly take a compass bearing. Then the mist closes in again.
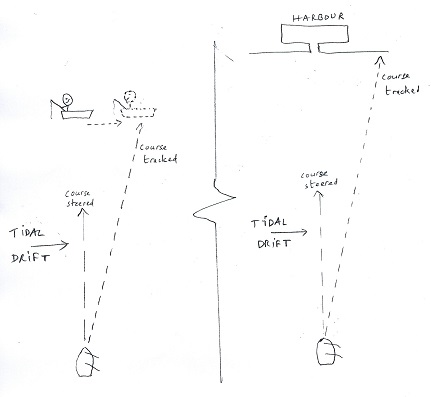
Now suppose instead that the sight you glimpsed through the mist was not a drifting boat, but a harbour entrance. In this case, if you take a compass bearing and then steer that heading thorough the mist, you will not successfully navigate to the harbour entrance. The harbour doesn’t drift with the tide. You have no rationale for ignoring the drift.
Summarising, we should ignore the drift when we have a rationale do so (in an option context: continuous hedging), and not ignore it when we don’t.
This analogy isn’t perfect. In particular, it doesn’t encompass (ha ha) the idea of a policy-driven reflecting barrier underpinning the assumed diffusion of house prices. But it’s a start. I welcome any suggestions for better analogies.