TLDR: When fractional shares (revenue by product, market shares by company, or similar quantities) are ranked and grouped in buckets, any ratio of successive bucket means >0.5 is suspect.
————–
Listening to this interview with John Hempton reminded me of his forensic scepticism about the following pie chart, taken from an investor presentation about the pharma company Valeant.
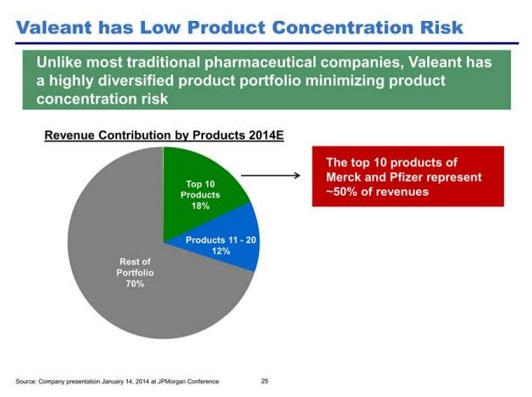

John wrote (in 2014, when Valeant was still ostensibly a very successful company) that the chart looked implausible
“What we are saying is the top ten products average 1.8 percent of sales each. The next ten average 1.2 percent.
Now lets just – for the sake of argument suggest that the top product is 3 percent of sales. And the next four average 2.3 percent. Well then the first five are 12.2 percent of sales – and the next five can only be 5.8 percent of sales (or they average 1.16 percent of sales).
But oops, that is too much concentration – because we know the next ten average 1.2 percent of sales. In fact it is far too much concentration as product number 11 needs to be more than 1.2 percent of sales.
I have fiddled with these numbers and they imply a distribution of sales flatter than I have ever seen in any product or category. In order to make the numbers work the differences between product sales have to be trivial all through the first fifteen products.”
This is an acute observation to make just skimming a presentation, and I’m not sure I would have got it. And what if the buckets (sectors on the pie chart) each contained 3 or 5 items instead of 10 – what difference would that make? Can we generalise this?
One way to think about it is to assume revenue shares by product form a geometric progression with a constant scaling factor, say r. E.g. if first product has 5% share, the second has 5 x 0.8 = 4% share, then the third has 4% x 0.8 = 3.2% share, etc. This won’t be exact in reality, but the sorting by size means it can’t be far off.
Then if the first term of the geometric progression – i.e. the share of the largest product – is x1, the usual formula for the sum of the first 10 terms is

and the mean over the first bucket is just this divided by ten.
We want to find {mean over bucket of first 10 / mean over bucket of next 10}. Replacing 10 by n for generality, some trivial algebra shows that this ratio of successive bucket means is given by

We can display this quantity in a 2-way look-up table against the scaling factor, r, and the number of items in each bucket, n:

For the original Valeant example, n = 10, and the observed ratio of successive bucket means is 1.2% / 1.8% ≈ 0.66. So reading off the top number in the third column, this implies a scaling factor of around 0.96, which seems incredibly flat. Hence John’s intuition that the chart looked dodgy.
More generally, what’s “dodgy” depends on what the true scaling factor is. E.g. If the largest holdings in an investor’s portfolio are sorted by size, this might typically give a scaling factor of 0.8 or less; but not if the investor constantly rebalances the portfolio to equal weights (which some people say is a good idea, although the maths is subtle and a lot of published work on “volatility pumping” is flawed). For most quantities, my intuition is that a scaling factor as high as 0.9 (the third row of the table) would be rare. It’s also striking how quickly the values fall away for lower (more typical?) scaling factors. Overall, the following seems a reasonable rule of thumb:
When fractional shares (revenue by product, market shares by company, or similar quantities) are sorted by size and grouped into descending buckets, any ratio of successive bucket means above 0.5 (or perhaps even 0.3) is suspect.